Preprocess to update-query in Subtree

Prerequisites:

In this tutorial, we will learn how to preprocess a given tree to update a node and query in a subtree using a data structure like segment tree.

A subtree of a tree T is a tree consisting of a node in T and all of its descendants in T.

We know there are well known data-structures to update and query in subarray of an array. We can use all of them to query in a subtree. Let’s see how we'll do that!

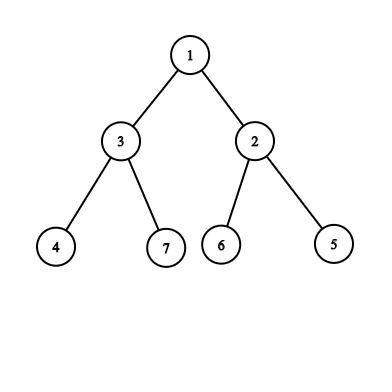
Suppose we have a tree with 7 node and the tree looks like following:

Let’s assume there is a value written in every node. For example, the numbers are as following:

Node Number

1

2

3

4

5

6

7

Assigned Value

9

10

11

6

8

12

5

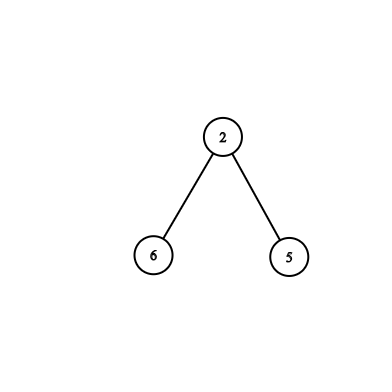
For example, a tree having node 2 as root is the subtree of the mentioned tree.

So, for an example, if we want to get the maximum value among that subtree, we need to find the maximum value among the nodes 2, 6 and 5.

Node Number

1

2

3

4

5

6

7

Assigned Value

9

10

11

6

8

12

5

As we are seeing, these node indexes do not build a segment, we are not able to use data-structures to find the maximum efficiently.

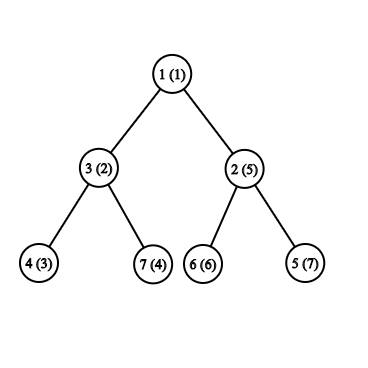
But there is a solution, let’s traverse the tree by dfs fashion and write the traversal order on these nodes.

Traversal Order

1

2

3

4

5

6

7

Node Number

1

3

4

7

2

6

5

Assigned Value

9

11

6

5

10

12

8

Now back to the query part, the candidate nodes of the query are highlighted as follows:

Traversal Order

1

2

3

4

5

6

7

Node Number

1

3

4

7

2

6

5

Assigned Value

9

11

6

5

10

12

8

Now we can see, the traversal order of these nodes form a segment and we can easily apply data-structure like segment tree to find the maximum of that subtree having node 2 as root.

The formula to get traversal order range for a subtree is

Explanation: If we go back to our example subtree, the left traversal order of the highlighted segment is 5, which is the traversal order of node 2, which is the root of the subtree. And as the right traversal order will be the last node of that subtree. This can be easily found by adding subtree size.

How we can traverse the tree in dfs fashion and finding subtree size related code are as follows:

int traversalOrder = 0;
int sz[Max];
int order[Max];
vector<int> adj[Max];

int dfs(int u) {
        order[u] = ++traversalOrder;
        sz[u] = 1;

        for(int v : adj[u]) {
                if (!order[v]) {
                        sz[u] += dfs(v);
                }
        }
        return sz[u];
}

And getting traversal order range for a subtree is as like follows:

pair<int, int> getRange(int root) {
        int rootTraversalOrder = order[root];
        int l = rootTraversalOrder;
        int r = rootTraversalOrder + sz[root] - 1;
        return {l, r};
}

Now we can update a node and query over a subtree using a data structure like segment tree.

Thank you for your reading. :D

Published on 05 December, 2020